Task 6: Simulation of phase separation phenomena

Task 6: Simulation of phase separation phenomena#

In this final task, we will use the Cahn-Hilliard solvers from Task 4 and Task 5 to study the dynamics of phase separation phenomena more closely, using realistic initial conditions and zero external forces.

The dynamics of phase separation phenomena are driven by the antagonist effects of mixing and interface energy. Due to its double-well potential, the mixing energy tends to drive the system away from the homogeneous state \(u=0\) towards the phase-separated states \(u=\pm 1\). On the other hand, the interface energy tends to minimize the total interfacial area between the two phases, as phase boundaries are regions of high energy where the field \(u\) exhibits large gradients to do its rapid change from \(+1\) to \(-1\). If the total energy of the system had been solely determined by the interface energy, the a completely homogeneous state would have been preferred. It is this competition between the two effects which leads to the formation of complex patterns and structures during the phase separation process. In the absence of external forces, the system evolves towards a state of minimal free energy, leading to the formation of distinct phases with characteristic length scales. This process is characterized by several distinct stages, including spinodal decomposition, nucleation and growth, and coarsening and Oswald ripening.

Spinodal decomposition and Ostwald ripening are two distinct mechanisms observed during phase separation phenomena. Spinodal decomposition occurs when a homogeneous mixture becomes unstable and spontaneously separates into distinct phases due to small fluctuations in composition. This process is characterized by the rapid formation of interconnected structures with a characteristic wavelength, driven by the reduction of free energy. In contrast, Ostwald ripening describes the later-stage coarsening process, where larger domains grow at the expense of smaller ones due to differences in chemical potential. This leads to a reduction in the total interfacial energy of the system, resulting in the growth of larger, more stable structures over time. Together, these processes illustrate the interplay between mixing energy and interface energy in driving phase separation dynamics.

The time scales for the spinodal decomposition and Ostwald ripening are determined by the characteristic length scale of the system, the mobility of the components, and the temperature of the system. In general, spinodal decomposition occurs on (much) shorter time scales, while Ostwald ripening occurs on longer time scales.

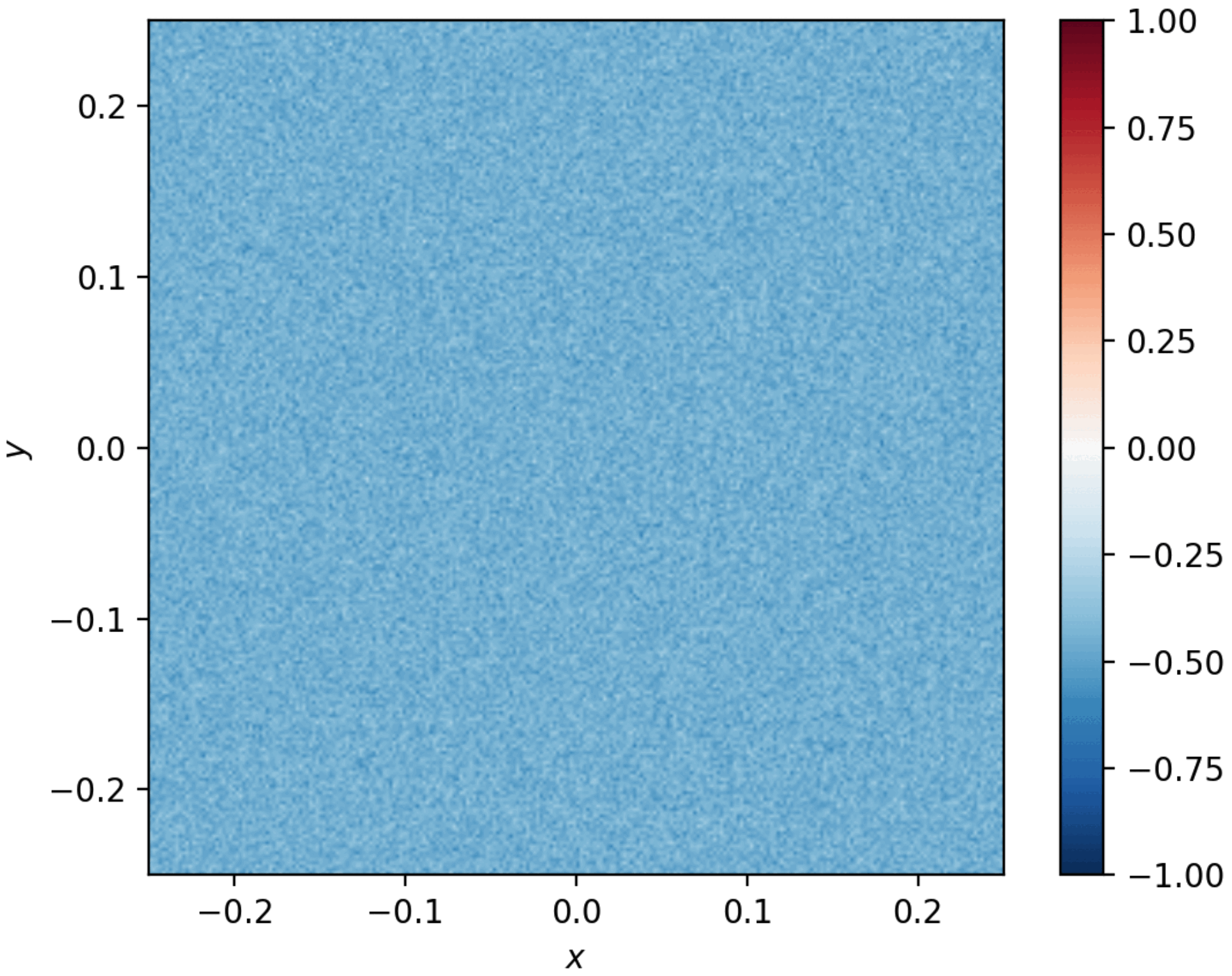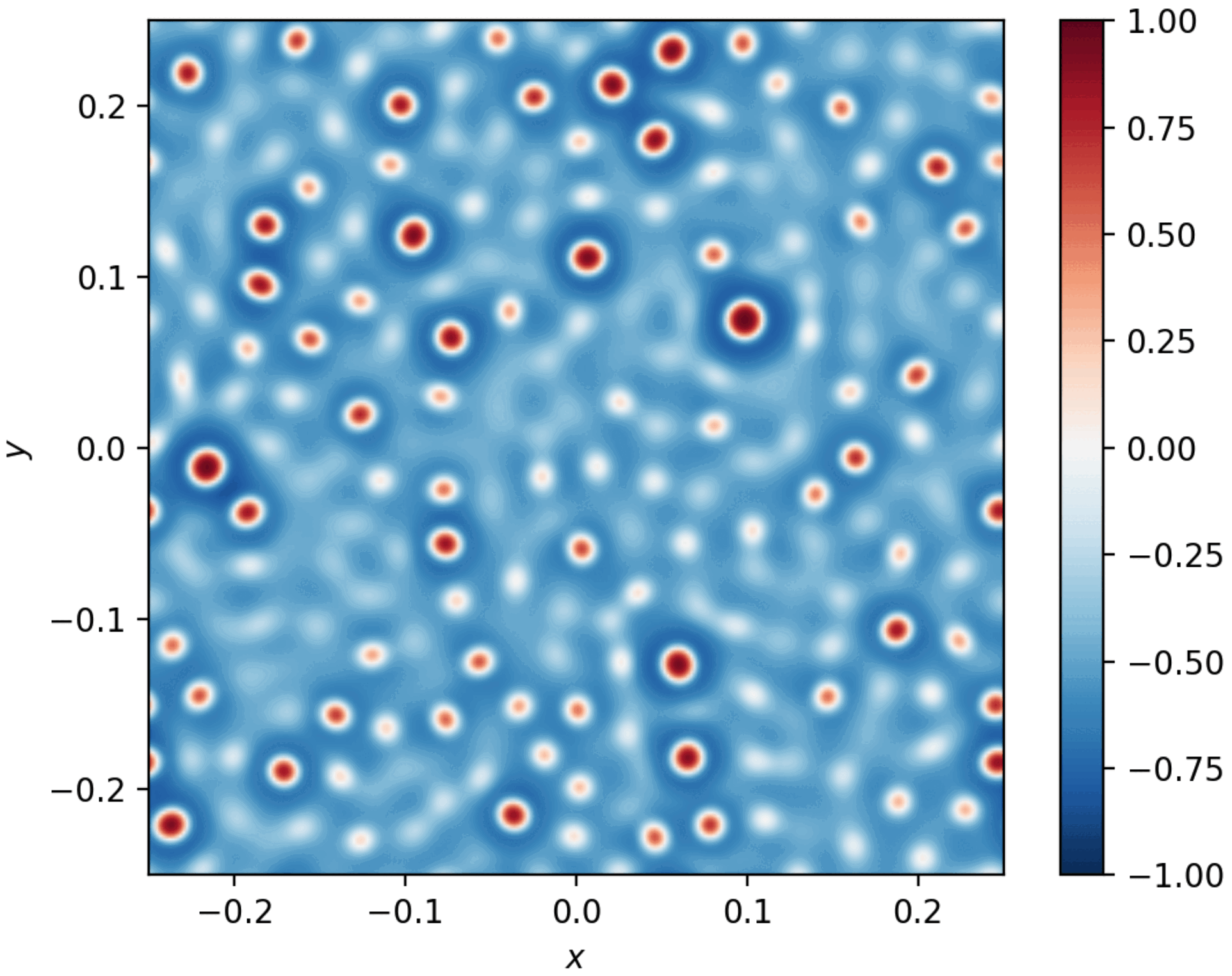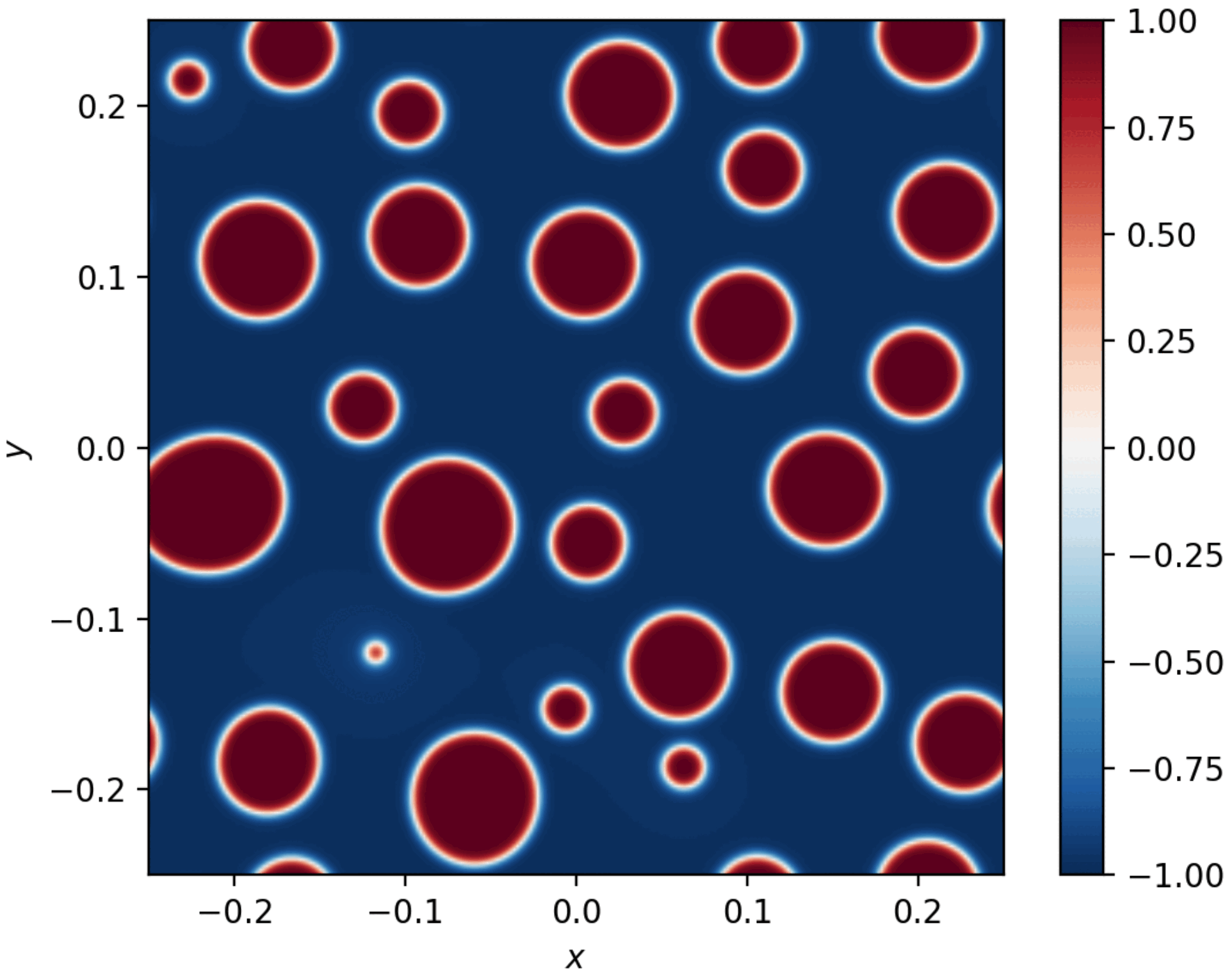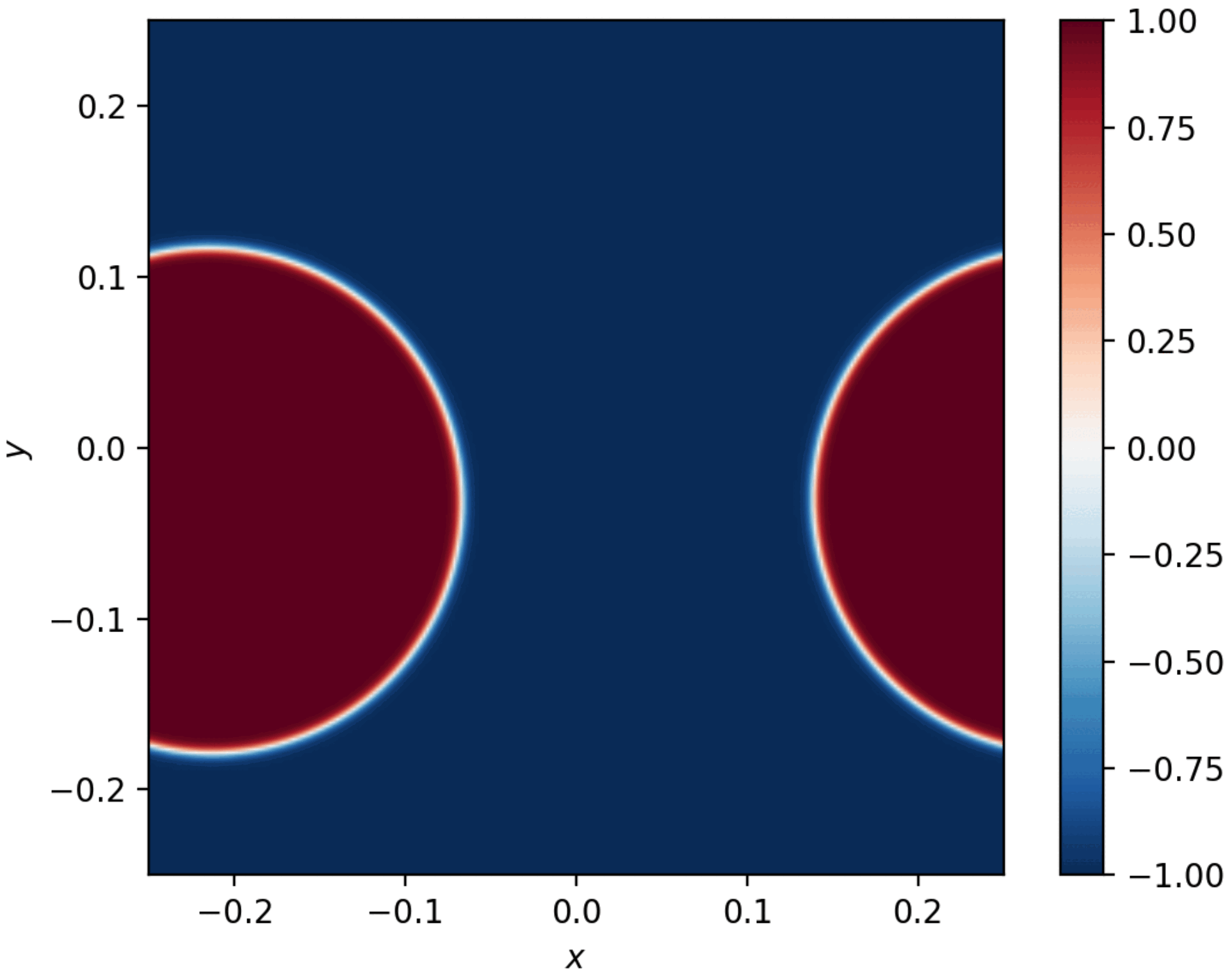Phase Separation Dynamics Figure. Combined snapshops illustrating initial spinodal decomposition and subsequent Ostwald ripening in a phase separation process. Note the animation is not linear in time, and the time between the shown snapshots is not constant (which you will find out when you run the simulation!).

The word “spinodal” is term from material science that describe the transformation of a system of two or more components in a metastable phase into two stable phases.

The word “Ostwald” refers to the German chemist Wilhelm Ostwald, who first described the ripening process in 1896.

To this end we want you to run a number of simulations of the Cahn-Hilliard equation based on following setup

  • Domain: \(\Omega = [0,0.5]^2\)

  • Time interval: \(I = [0,4.0]\), and \(I = [0,0.01]\)

  • Spatial resolution: \(Nx = Ny = 256\)

  • \(\kappa = 0.0025^2\)

  • two different initial conditions:

    (92)#\[\begin{align} u_0(x,y) &= 0.05\mathrm{rand}(x,y) \\ u_0(x,y) &= -0.45 + 0.05\mathrm{rand}(x,y) \end{align}\]

  • Two different time step sizes \(\tau \in \{10^{-3}, 10^{-4}\}\)

The first initial condition is a random perturbation of the base state \(u_0(x,y) = 0.0\), and can produced by the following code snippet:

rng = np.random.default_rng(12345)
noise = 0.05
u0_base = 0.0
U0 = np.ones_like((Ny, Nx))
U0 = np.full((Ny, Nx), u0_base) +  noise*rng.standard_normal((Ny, Nx))

Please use the random seed 12345 used above to make your code reproducible and the results comparable.

For each simulation the following tasks should be performed:

  • Plot the total mass \(\int_{\Omega} u \,\mathrm{d}x\) of the concentration field \(u\) at each time step.

  • Plot both the mixing energy, the interface energy and the total energy of the system at each time step.

  • Generate a number of snapshots of the concentration field \(u\) at different time steps.

Don’t forget to explain how you calculate both the total mass and the energies!

Hint. It might be useful to create an animation/movie of the snapshots to inspect the dynamics of the phase separation more closely. When you generate animations, do not more than 200-400 frames, otherwise the creation of the animation will just take too long.

Discuss the results with respect the two different initial conditions, the two different time step sizes, and the two different solvers. In particular, you should think about the following questions:

  • How does the total mass of the concentration field evolve in time?

  • How does the mixing energy, the interface energy and the total energy of the system evolve in time?

  • Can you spot any differences in the evolution of the energies for the two different initial conditions? If so, can you relate those to the evolution of the snapshots?

  • How does the time step size influence the evolution of the energies and the snapshots?

  • How does solver choice influence the evolution of the energies and the snapshots?

  • Identify roughly when the spinodal decomposition and the Ostwald ripening occur in the simulations? At which time does the evolution slows down siginificantly? And when does the system reach am equilibrium state?

When you have identified roughly the time scale \([0, T_{sd}]\) for the spinodal decomposition, rerun the simulation with your favorite/best working solver for a time interval \(I = [0, T_{sd}]\) using \(40000\) time steps.

Finally, we want you to generate and include an animated gif image combining 3-5 snapshots of the concentration field \(u\) during the spinodal decomposition and \(3\)-\(5\) snapshots from Ostwald ripening process including on of the final equilibrium state.

Note. If your Song based solver is not working properly, fall back to the simpler IMEX solver from Task 4 to run the simulations.

HAVE FUN!